Introduction to EIP-4844

EIP-4844 introduces a new transaction type called “Blob-carrying transaction”. These transactions contain a large quantity of data that, while not directly accessible through the EVM execution layer, have their commitment readable in a specific format from the execution layer. The design aims for full compatibility with the data format proposed in the sharding solution.

From a mathematical standpoint, each blob is a vector composed of 4096 finite field elements. In EIP-4844, this finite field is chosen as the scalar field of the elliptic curve BLS12–381. To commit a blob, the corresponding vector is interpolated into a polynomial with a degree of 4095.

Assuming i ranges from 0 to 4095 and ω is the 4096-th primitive root of unity in the BLS12–381 scalar field, the i-th coordinate is evaluated as ω^i. Employing the general computational logic of the KZG commitment scheme on this polynomial allows for the derivation and verification of blob commitments on Ethereum.

EIP-4844 will play a pivotal role in the rollup process. Prior to this proposal, transaction data was stored as calldata and public inputs, incurring high gas costs. With EIP-4844, raw transaction data is encapsulated into blobs and stored as ”Blob-data” within the consensus layer, And can be discarded after a certain period. This mechanism ensures data availability for the required duration, fulfilling the completeness requirements of layer 2.

Equivalent Proof of KZG Commitment

EIP-4844 introduces complex requirements for ZK-rollups , focusing on ensuring the consistency between blob commitments and the underlying transaction data. According to the current development state of Ethereum, the existing precompiled contracts only support the pairing operation (ecPairing) and group operations(ecMul, ecAdd) about BN254 curve,However, the elliptic curve used in EIP-4844 is BLS12–381.

This discrepancy necessitates adaptations in the zk-circuit design to accomodate the operations on BLS12–381 through BN254 equivalents, leveraging the Schwartz-Zippel lemma for commitment validation. The commitment to the blob data will be converted to a random challenge on the evaluation of an arbitrary point of the interpolated polynomial.

There are three parts of the equivalent proof:

• Prove that the interpolated polynomial (finite field elements) stored in the blob data indeed represents exactly the raw transaction data using circuits.
• Prove that the interpolated polynomial passes the evaluation challenge on a random point.
• Prove that both theKZG commitment and the circuit’s public inputs adhere to the expected constraints through the precompiled contract (point_evaluation_precompile()) in EIP-4844.

Equivalence of Blob Data and Raw Transaction Data

For ZK circuits, our starting point is with an illustration of one blob. In zero-knowledge terminology, the circuit’s public inputs have two components: the raw transaction data and the 4096 elements within the target finite field. The core logic here involves encoding, which converts transaction data into blob data. here’s a concise explanation of our encoding approach:

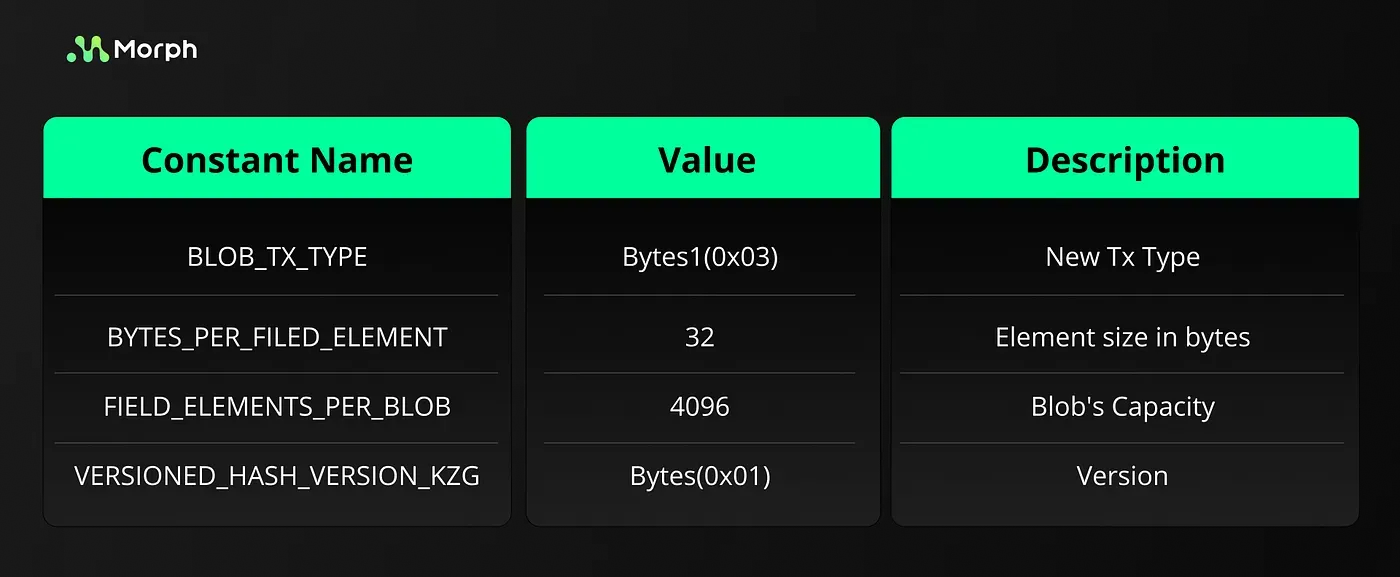
• We encode the field elements as big-endian uint256, specifically within the BLS12–381 modulus range. This process transforms 31-byte data into 32-byte data. To support the follow-up blob-sharding verification, we segment the raw transaction data of a batch into chunks.
• Within each chunk, we generate a one 31-byte piece of data, labeled as D. The total length of the chunk’s input data is stored in the foremost 4 bytes of D. The remaining 27 bytes of D are filled with the actual chunk data, starting from the beginning. After assembling D, we embed a 1-byte prefix of zero to produce the first field element of this chunk’s respective blob, which is a 32-byte unit.
• For the remaining portion of the chunk, we embed a one-byte zero in each 31-byte data sequence and regard this 32-byte sequence as one field element. When the last segment of data is less than 31 bytes, it’s formatted to 31-bytes and treated in the same manner.

This method splits the batch’s original data into multiple sharding units, each corresponding to the length of a chunk, and stores them as blob data within each chunk. Compared to previous methods, this encoding scheme enhances subsequent data aggregation processes.

Verification of the Interpolated Polynomial’s Evaluation

To streamline and reduce the complexity of wrong-field arithmetic operations, it’s crucial to establish that the interpolated polynomials are equal both within the circuit and the contract. The more challenging aspect lies in circuit evaluation, where the Barycentric interpolation formula presents a viable solution. This method depends solely on non-native multiplications and divisions.

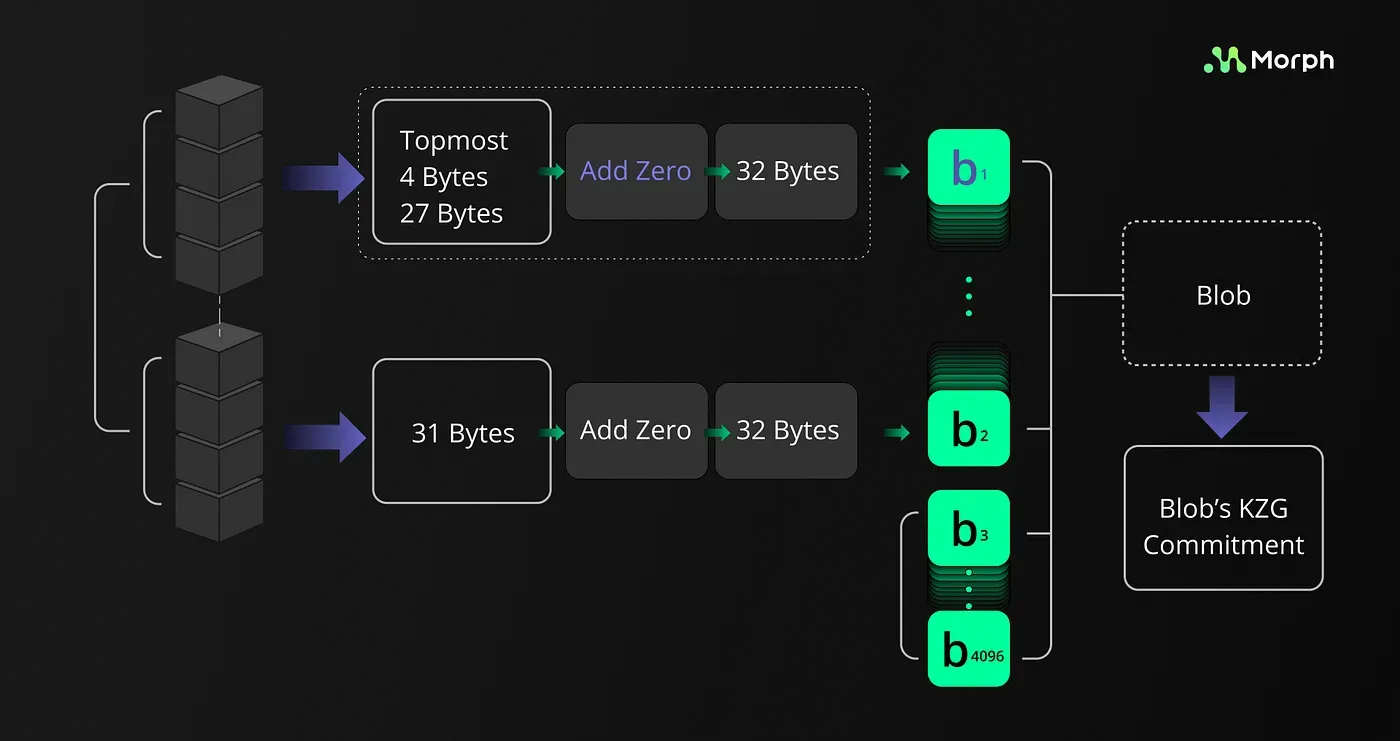
When considering a specific blob, the public inputs of the circuit contain 4096 scalar field elements, the challenge point ‘x’ and an evaluation result ‘y’.

Given a blob containing 4096 scalar field elements:

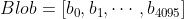
Formula:

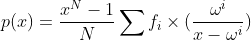
the Barycentric interpolation formula could be written as:

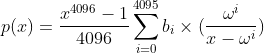
This approach is applied under the following computational constraints:

• Utilizing the Fiat-Shamir transformation, a pseudo-random challenge point x is generated, with its consistency verified against a Poseidon Hash within the circuit.
• Check if:

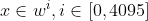
and compute the Barycentric formula if satisfied

• Check if the result equals y

Aggregation Circuit

In our encoding approach, we translate each 32-byte transaction data into a single finite field element within the BLS12–381 scalar field. However, the length of raw transaction data may not always fit neatly into 32-byte increments, leading to potential issues:

• The transaction data within a chunk might not precisely equate to a whole number ofl finite field elements.
• After encoding, some transaction data may span across two separate blobs.
• Occasionally, a chunk may only contain a small amount of raw transaction data, resulting in significantly fewer than 4096 finite field elements.

To address the first problem, we embed zeros to each chunk’s transaction data, ensuring these align to the 32-byte boundaries.

To manage data spanning multiple blobs, the tail end of one blob’s transaction data may commence the first element of the next blob. A multi-open approach for KZG commitments aggregated verification across blobs.

For chunks with minimal data, the encoding scheme incorporates additional information to leverage aggregated evaluation circuits effectively:

• We adjust to store chunk-length information, rather than Batch-length, within the initial bits of each chunk’s raw data before encoding.
• Each chunk includes two extra indices for constraint and consistency checks: the indices of the chunk’s first and last transactions.

Explaining the Aggregated Methodology Evaluation:.

Consider a blob with its finite field elements encoded transaction data across multiple chunks, totaling 4096 elements. If k represents the total number of chunks, with the i-th chunk equating to the following finite field elements:

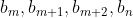
We could first compute:

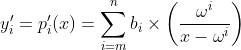
For a singular blob and its corresponding k chunk,s for example, we aggregate chunk-specific proofs using the equation above for:

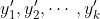
, and aggregate them in the same blob:

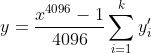
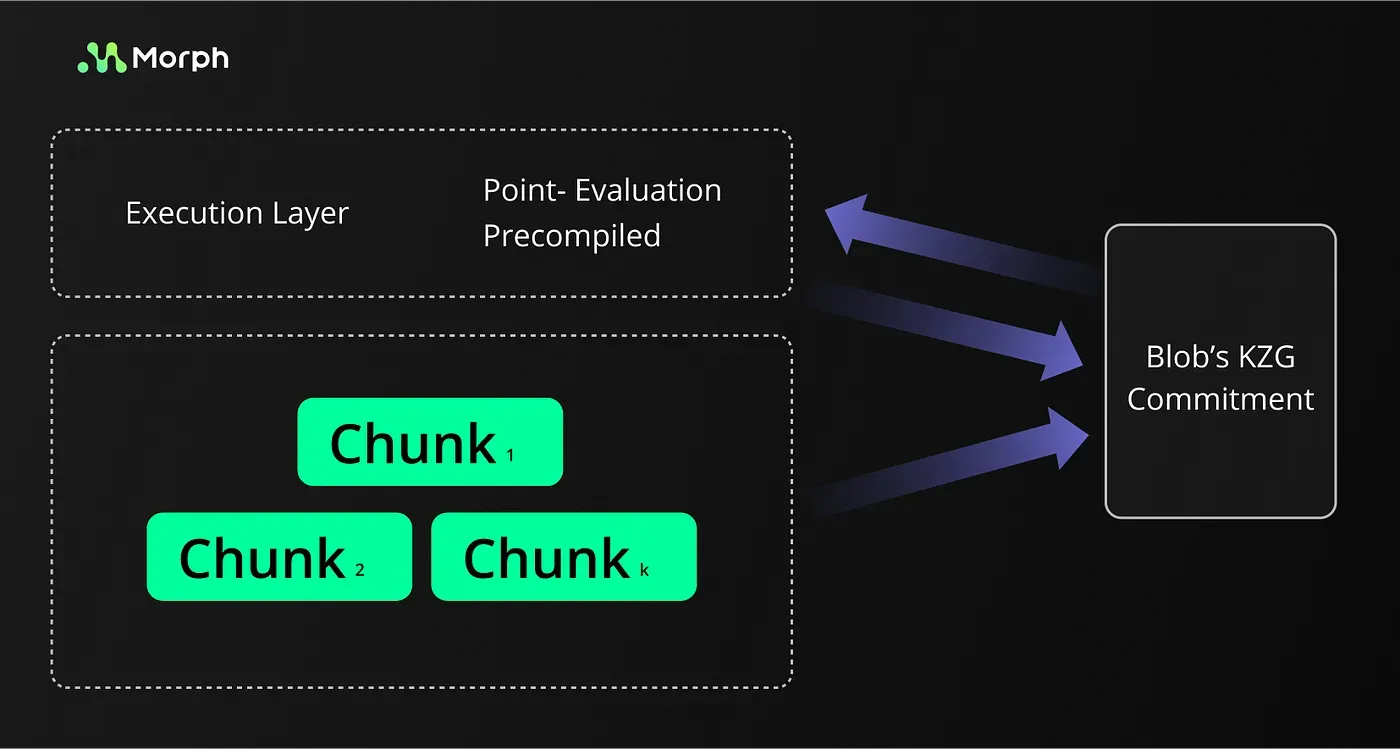
Verification On the Smart Contract

EIP-4844 introduces a new precompile that enables smart contracts to open the commitment to blobs. This allows for a consistency check between the blob data and its commitment, simplifying to a comparison between the challenge point x, its evaluation y, and the Blob’s commitment. Smart contracts can verify this by confirming p(x) = y.

Summary

Layer-2 solutions play an important role in Ethereum’s scaling roadmap, though they often raise concerns about security or poor performance. Rooted in solid mathematical principles, ZK-rollups offer high security and performance, albeit with challenges in proof generation and verification. Through algorithmic improvements and better hardware, the proof generation burden can be alleviated, and the blockchain’s involvement can enhance verification efficiency.

Our proposal has the following three advantages under EIP-4844:

• Compatibility: We’ve outlined a method for filling blob data, shifting from batch-level to chunk-level encoding, ensuring seamless integration with the existing zkEVM circuits and EIP-4844.
• Practicality: Given the current precompiles support operations over BN254 (not BLS12–381 as EIP-4844uses), we face implementation and performance challenges in verifying KZG commitments. The Barycentric formula minimizes these wrong-field operations to manageable computations.
• Aggregability: Aggregating proofs lowers both the number of proofs required and the on-chain gas costs for verification. Taking advantage of our design at a chunk-aggregation level, we maximize efficiency under EIP-4844.

EIP-4844 is an ultimate catalyst that pushes progression in ZK-rollups, raising potential challenges and solutions alike. This article outlines our practical approach to circuit design with EIP-4844, Aiming for a cheaper and safer transaction environment. The Morph continues to explore new technologies, contributing to broader community efforts.

About Morph

Morph is a consumer Layer-2 blockchain. Combining the best of OP and ZK rollups, it offers unmatched scalability and security, aiming to lay a foundation for an ecosystem of consumer-focused, value-driven DApps.

Through its hallmark features, such as a Decentralized Sequencer Network, Responsive Validity Proof (RVP) system, and modular design, the project delivers efficient and flexible scaling while preserving the initial security, availability, and compatibility of the Ethereum network.